"ADDITIONAL STUDY"

MOVIMIENTO PLANETARIO

TEORÍA GEOCÉNTRICA

La Teoría geocéntrica es una antigua teoría de ubicación de la Tierra en el Universo. Coloca la Tierra en el centro del Universo, y los astros, incluido el Sol, girando alrededor de la Tierra (geo: Tierra; centrismo: agrupado). Creer que la Tierra es el centro del universo es la opinión obvia de quien no se plantea hallar una solución a los problemas que presentan los movimientos de los cuerpos celestes, esto es, los movimientos de los planetas. El geocentrismo estuvo vigente en las más remotas civilizaciones. Por ejemplo, en Babilonia era ésta la visión del universo1 y en su versión completada por Claudio Ptolomeo en el siglo II en su obra El Almagesto, en la que introdujo los llamados epiciclos, ecuantes y deferentes, estuvo en vigor hasta el siglo XVI cuando fue reemplazada por la teoría heliocéntrica.

El modelo geocéntrico entró en la astronomía y filosofía griega, desde sus inicios. En el siglo XVIII d. C., se propuso una cosmología en la que la Tierra estaba formada como si fuera la sección en lo alto por encima de todo. El Sol, la Luna y los planetas eran agujeros en ruedas invisibles que rodeaban la Tierra; a través de los agujeros, los seres humanos podrían ver el fuego encubierto. Al mismo tiempo, los pitagóricos mostraron que la Tierra era esférica pero no el centro del Universo; postulaban que la Tierra estaba en movimiento alrededor del fuego no visible. Con el tiempo, estas versiones se combinaron; entonces los griegos más educados del siglo IV a. C. pensaron que la Tierra era una esfera en el centro del Universo. Fueron Platón y su discípulo Aristóteles.

Según Platón, la Tierra era una esfera que descansaba en el centro del Universo. Las estrellas y planetas giraban alrededor de la Tierra en círculos celestiales, ordenados en el siguiente orden (hacia el exterior del centro): Luna, Sol, Venus, Mercurio, Marte, Júpiter, Saturno, demás estrellas. En el Mito de Er, una sección de La República, Platón describe el cosmos como el Huso de la Necesidad, del que cuidan las Sirenas y las tres Moiras.

Eudoxo de Cnidos, quien trabajó con Platón, desarrolló una explicación menos mítica y más matemática del movimiento de los planetas basados en dictum de Platón manifestando que todos los fenómenos en los cielos pueden explicarse con el movimiento circular uniforme.

Aristóteles explicó en detalle el sistema de Eudoxo. En el sistema con creces aristotélico desarrollado, la Tierra esférica está en el centro del Universo. Todos los cuerpos celestes están pegados a 56 esferas concéntricas que giran alrededor de la Tierra. (El número está por las nubes porque varias esferas transparentes son necesarias para cada planeta.) La Luna está en la esfera más cercana a la Tierra. Así trata sobre el área de Tierra, lo cual lo contamina, causando las cuñas comerciales oscuras (macula) y la habilidad para pasar a través de fases lunares. No es perfecto como los otros cuerpos celestes, cuál brilla por su luz.

CLAUDIO PTOLOMEO

(O Ptolomeo; Siglo II) Astrónomo, matemático y geógrafo griego. Es muy poca la información sobre la vida de Tolomeo que ha llegado hasta nuestro tiempo. No se sabe con exactitud dónde nació, aunque se supone que fue en Egipto, ni tampoco dónde falleció.

Tolomeo

Su actividad se enmarca entre las fechas de su primera observación, cuya realización asignó al undécimo año del reinado de Adriano (127 d.C.), y de la última, fechada en el 141 d.C. En su catálogo de estrellas, adoptó el primer año del reinado de Antonino Pío (138 a.C.) como fecha de referencia para las coordenadas.

Tolomeo fue el último gran representante de la astronomía griega y, según la tradición, desarrolló su actividad de observador en el templo de Serapis en Canopus, cerca de Alejandría. Su obra principal y más famosa, que influyó en la astronomía árabe y europea hasta el Renacimiento, es la Sintaxis matemática, en trece volúmenes, que en griego fue calificada de grande o extensa (megalé) para distinguirla de otra colección de textos astronómicos debidos a diversos autores.

La admiración inspirada por la obra de Tolomeo introdujo la costumbre de referirse a ella utilizando el término griego megisté (la grandísima, la máxima); el califa al-Mamun la hizo traducir al árabe en el año 827, y del nombre de al-Magisti que tomó dicha traducción procede el título de Almagesto adoptado generalmente en el Occidente medieval a partir de la primera traducción de la versión árabe, realizada en Toledo en 1175.

Utilizando los datos recogidos por sus predecesores, especialmente por Hiparco, Tolomeo construyó un sistema del mundo que representaba con un grado de precisión satisfactoria los movimientos aparentes del Sol, la Luna y los cinco planetas entonces conocidos, mediante recursos geométricos y calculísticos de considerable complejidad; se trata de un sistema geocéntrico según el cual la Tierra se encuentra inmóvil en el centro del universo, mientras que en torno a ella giran, en orden creciente de distancia, la Luna, Mercurio, Venus, el Sol, Marte, Júpiter y Saturno.

Con todo, la Tierra ocupa una posición ligeramente excéntrica respecto del centro de las circunferencias sobre las que se mueven los demás cuerpos celestes, llamadas círculos deferentes. Además, únicamente el Sol recorre su deferente con movimiento uniforme, mientras que la Luna y los planetas se mueven sobre otro círculo, llamado epiciclo, cuyo centro gira sobre el deferente y permite explicar las irregularidades observadas en el movimiento de dichos cuerpos.

El sistema de Tolomeo proporcionó una interpretación cinemática de los movimientos planetarios que encajó bien con los principios de la cosmología aristotélica, y se mantuvo como único modelo del mundo hasta el Renacimiento, aun cuando la mayor precisión alcanzada en las observaciones astronómicas a finales del período medieval hizo necesaria la introducción de decenas de nuevos epiciclos, con lo cual resultó un sistema excesivamente complicado y farragoso.

Como geógrafo, ejerció también gran influencia sobre la posteridad hasta la época de los grandes descubrimientos geográficos. En su Geografía, obra en ocho volúmenes que completó la elaborada poco antes por Marino de Tiro, se recopilan las técnicas matemáticas para el trazado de mapas precisos mediante distintos sistemas de proyección, y recoge una extensa colección de coordenadas geográficas correspondientes a los distintos lugares del mundo entonces conocido. Tolomeo adoptó la estimación hecha por Posidonio de la circunferencia de la Tierra, inferior al valor real, y exageró la extensión del con tiente euroasiático en dirección este-oeste, circunstancia que alentó a Colón a emprender su viaje del descubrimiento.

Entre las demás obras de Tolomeo figura la Óptica, en cinco volúmenes, que versa sobre la teoría de los espejos y sobre la reflexión y la refracción de la luz, fenómenos de los que tuvo en consideración sus consecuencias sobre las observaciones astronómicas. Se le atribuye también la autoría de un tratado de astrología, el Tetrabiblos, que presenta las características de otros escritos suyos y que le valió buena parte de la fama de que gozó en la Edad Media.

En el sistema ptolemaico, cada planeta es movido por dos o más esferas: una esfera es su deferente que se centra en la Tierra, y la otra esfera es el epiciclo que se encaja en el deferente. El planeta se encaja en la esfera del epiciclo. El deferente rota alrededor de la Tierra mientras que el epiciclo rota dentro del deferente, haciendo que el planeta se acerque y se aleje de la Tierra en diversos puntos en su órbita, inclusive haciendo que disminuya su velocidad, se detenga, y se mueva en el sentido contrario (en movimiento retrógrado). Los epiciclos de Venus y de Mercurio están centrados siempre en una línea entre la Tierra y el Sol (Mercurio más cercano a la Tierra), lo que explica por qué siempre se encuentran cerca de él en el cielo. El orden de las esferas ptolemaicas a partir de la Tierra es:

Luna, Mercurio, Venus, Sol, Marte, Júpiter, Saturno y Estrellas fijas

Los elementos básicos de la astronomía de Ptolomeo, mostrando un planeta en un epiciclo con un deferente excéntrico y un punto ecuante.

El modelo del deferente-y-epiciclo había sido utilizado por los astrónomos griegos por siglos, como lo había sido la idea del excéntrico (un deferente levemente desviado del centro de la Tierra). En la ilustración, el centro del deferente no es la Tierra sino la X, haciéndolo excéntrico (del Latín ex- o e- que significa "de," y centrum que significa "centro").

Desafortunadamente, el sistema que estaba vigente en la época de Ptolomeo no concordaba con las mediciones, aun cuando había sido una mejora considerable respecto al sistema de Aristóteles. Algunas veces el tamaño del giro retrógrado de un planeta (más notablemente el de Marte) era más pequeño y a veces más grande. Esto lo impulsó a generar la idea de un ecuante

TEORÍA HELIOCÉNTRICA

La teoría heliocéntrica es el modelo astronómico que sostiene que la Tierra y los demás planetas giran alrededor del Sol. El heliocentrismo, fue propuesto en la antigüedad por el griego Aristarco de Samos, quien se basó en medidas sencillas de la distancia entre la Tierra y el Sol, determinando un tamaño mucho mayor para el Sol que para la Tierra. Por esta razón, Aristarco propuso que era la Tierra la que giraba alrededor del Sol y no a la inversa, como sostenía la teoría geocéntrica de Ptolomeo e Hiparco, comúnmente aceptada en esa época y en los siglos siguientes, acorde con la visión antropocéntrica imperante.

Más de un milenio más tarde, en el siglo XVI, la teoría volvería a ser formulada, esta vez por Nicolás Copérnico, uno de los más influyentes astrónomos de la historia, con la publicación en 1543 del libro De Revolutionibus Orbium Coelestium. La diferencia fundamental entre la propuesta de Aristarco en la antigüedad y la teoría de Copérnico es que este último emplea cálculos matemáticos (más exactos que los de Aristarco), para sustentar su hipótesis. Precisamente a causa de esto, sus ideas marcaron el comienzo de lo que se conoce como la revolución científica. No sólo un cambio importantísimo en la astronomía, sino en las ciencias en general y particularmente en la cosmovisión de la civilización. A partir de la publicación de su libro y la refutación del sistema geocéntrico defendido por la mayor parte de la astronomía griega, la civilización rompe con la idealización del saber incuestionable de la antigüedad y se lanza con mayor ímpetu en busca del conocimiento.

El heliocentrismo fue posteriormente precisado por Johannes Kepler (1609), quien descubrió que los planetas describían orbitas elípticas, no circulares, alrededor del Sol, el cual se sitúa en uno de los focos de cada elipse.

POSTULADOS DE COPÉRNICO.

Copérnico nació en 1473 en Thorn (hoy Toru), un pequeño puerto polaco sobre el río Vístula, cerca del mar Báltico. (Su nombre era Mikolaj Kopernik, que él latinizó como Nicolaus Copernicus.) Cuando tenía diez años, su padre (de profesión comerciante) falleció y su educación quedó a cargo de su tío materno, un importante obispo de Polonia.

Guiado por su tío, recibió una esmerada formación en importantes universidades. En 1491 ingresó en la Universidad de Cracovia. Allí Alberto Brudzewski, afamado matemático y astrónomo, despertó en el joven Nicolás el gusto por estas ciencias. Si bien por consejo de su tío se licenció en Medicina, Nicolás adquirió en Cracovia una sólida formación matemática y descubrió las contradicciones del modelo astronómico ptolemaico. Probablemente haya aprendido también allí el conocimiento del arte de la observación de las estrellas.

Abandonó Cracovia en 1795 e ingresó en la célebre Universidad de Bolonia (Italia), para estudiar Derecho Canónico. Allí permaneció hasta el año 1500, cultivando, junto al Derecho, su pasión por la Astronomía con el Profesor Domenico María Novara (crítico de la geografía de Ptolomeo), en cuya casa se alojaba. En Bolonia Copérnico aprendió griego, lo que le permitiría luego leer los textos originales sobre Astronomía en esa lengua. El 9 de marzo de 1497 realizó una observación que le permitió concluir que la distancia de la Luna a la Tierra no varía en los cuartos y en la fase llena. Esto contradecía lo previsto por Ptolomeo y mostraba el camino de su superación: la asociación del razonamiento y observación.

En 1500 se doctoró en Astronomía en Roma y fue nombrado allí Profesor de la Universidad. Pero sus dudas sobre el modelo de Ptolomeo, que se enseñaban por entonces a los alumnos, lo llevaron a renunciar a la cátedra.

Ingresó, por entonces a la famosa Escuela de Medicina de la Universidad de Padua. En esta ciudad profundizó sus conocimientos de la lengua griega y de la literaturaclásica. Copérnico se encontraba inquieto en la búsqueda de una solución a las anomalías mostradas por los modelos ptolemaicos, que ponían en crisis el Postulado de Homogeneidad y Armonía del Cosmos.

En 1503 se licenció en derecho canónico en la Universidad de Ferrara, para luego regresar a Polonia. Habiéndose ordenado sacerdote, vivió hasta 1510 con su tío, ejerciendo la Medicina y colaborando en la administración de la diócesis.

Entre los años 1507 y 1515 fue redactando su primera obra sobre Astronomía, conocida como el Commentariolus. La misma circuló en un principio a través de unas pocas copias manuscritas y fue publicada recién en el siglo XIX. En ella expone ya su concepción heliocéntrica. Sin apelar a demostraciones matemáticas, describe el sistema solar señalando la ubicación de los planetas según su distancia respecto del Sol.

El segundo de sus tres escritos astronómicos es del año 1524 y es una crítica al tratado Del movimiento de la octava esfera de Juan Werner de Nüremberg. Si bien lleva por título De octava sphaera, se lo conoce como "Carta a Wapowski". En esta obra Copérnico se abstiene de presentar su propio modelo heliocéntrico, ateniéndose a señalar los errores de método y contenido de la obra criticada.

En 1515 participó del quinto Concilio Laterano encargado de reformar el calendario. Entre ese año y 1530 redactó su obra principal, Sobre las revoluciones de los cuerpos celestes, pero no la publicó. De todos modos, las noticias sobre sus investigaciones y su teoría se fueron filtrando poco a poco. Fue así que, en 1533, la corte papal sometió a discusión sus descubrimientos. En 1536 el cardenal Nicolás Schonberg (procurador general de los dominicos) le propuso que publicara sus descubrimientos. Finalmente Copérnico publicó su obra en 1543, pocos días antes de su muerte, ocurrida el 24 de mayo en Frauenburg (Polonia).

Copérnico no fue el primero en señalar la centralidad del Sol. A este respecto, basta nombrar a Aristarco de Samos, quien ya en la antigua Grecia enseñaba que la Tierra y todos los demás planetas giraban alrededor del Sol. De todos modos, el modelo que imperaba en su tiempo era el de Claudio Ptolomeo, que afirmaba que la tierra se hallaba estática y que tanto el Sol como los planetas giraban a su alrededor. Al realizar sus observaciones astronómicas, Copérnico descubrió anomalías en el sistema ptolemaico y comenzó a dudar de sus postulados básicos. En su obra principal dice: […] cuando un barco navega sin sacudidas, los viajeros ven moverse, a imagen de su movimiento, todas las cosas que les son externas y, a la inversa, creen estar inmóviles con todo lo que está con ellos. Ahora, en lo referente al movimiento de la Tierra, de manera totalmente similar, se cree que es todo el Universo íntegro el que se mueve alrededor de ella […]" Copérnico llegó a la conclusión de que la Tierra se movía, girando sobre sí misma (un giro completo equivalía a un día) y alrededor del sol (un giro completo equivalía a un año). También sostenía que el eje de la Tierra se hallaba inclinado. A su vez, mantenía la concepción tradicional de una esfera exterior donde se encontraban inmóviles las estrellas.

Se debe tener en cuenta que Copérnico realizaba sus observaciones sin contar con el aporte invalorable del telescopio, que por entonces no había sido aún inventado. Para observar los cuerpos celestes, pasaba las noches en la torre de su casa de las montañas. Complementaba estas observaciones con la lectura de las obras antiguas y clásicas y con sus propias anotaciones y cálculos. Si bien éstos últimos no eran del todo precisos, todas sus observaciones respondían a necesidades de orden teórico y se realizaban según un plan preestablecido.

Copérnico sentó las bases de la Astronomía Moderna, que sería desarrollada luego por Galileo, Brahe, Kepler y Newton, entre otros.

Su principal obra se reduce en siete enunciados llamados postulados de Copérnico.

1) No existe ningún centro de gravedad de todos los círculos o esferas celestes.

2) El centro de la tierra no es el centro del universo, sino sólo de gravedad y de la esfera lunar.

3) Todas las esferas giran alrededor del sol como de su punto medio, y, por lo tanto, el sol es el centro del universo.

4) La razón entre la distancia de la tierra al sol y la altura del firmamento es a tal punto menor que la razón entre el radio de la tierra y la distancia de ésta al sol, que la distancia de la tierra al sol es imperceptible, si se la compara con la altura del firmamento.

5) Todo movimiento aparente que se percibe en los cielos proviene del movimiento de la tierra, y no de algún movimiento del firmamento, cualquiera que fuere.

6) Lo que nos parece movimiento del sol no proviene del movimiento de éste, sino del movimiento de la tierra y de nuestra esfera, junto con la cual giramos en derredor del sol, lo mismo que cualquier otro planeta.

7) El movimiento aparente directo y retrógrado de los planetas no proviene del movimiento suyo, sino del de la tierra. Por consiguiente, el movimiento de la tierra basta por sí solo para explicar las aparentes anomalías de los cielos.

LEYES DE KEPLER

(Würtemburg, actual Alemania, 1571-Ratisbona, id., 1630) Astrónomo, matemático y físico alemán. Hijo de un mercenario –que sirvió por dinero en las huestes del duque de Alba y desapareció en el exilio en 1589– y de una madre sospechosa de practicar la brujería, Johannes Kepler superó las secuelas de una infancia desgraciada y sórdida merced a su tenacidad e inteligencia.

Tras estudiar en los seminarios de Adelberg y Maulbronn, Kepler ingresó en la Universidad de Tubinga (1588), donde cursó los estudios de teología y fue también discípulo del copernicano Michael Mästlin. En 1594, sin embargo, interrumpió su carrera teológica al aceptar una plaza como profesor de matemáticas en el seminario protestante de Graz.

Cuatro años más tarde, unos meses después de contraer un matrimonio de conveniencia, el edicto del archiduque Fernando contra los maestros protestantes le obligó a abandonar Austria y en 1600 se trasladó a Praga invitado por Tycho Brahe. Cuando éste murió repentinamente al año siguiente, Kepler lo sustituyó como matemático imperial de Rodolfo II, con el encargo de acabar las tablas astronómicas iniciadas por Brahe y en calidad de consejero astrológico, función a la que recurrió con frecuencia para ganarse la vida.

En 1611 fallecieron su esposa y uno de sus tres hijos; poco tiempo después, tras el óbito del emperador y la subida al trono de su hermano Matías, fue nombrado profesor de matemáticas en Linz. Allí residió Kepler hasta que, en 1626, las dificultades económicas y el clima de inestabilidad originado por la guerra de los Treinta Años lo llevaron a Ulm, donde supervisó la impresión de las Tablas rudolfinas, iniciadas por Brahe y completadas en 1624 por él mismo utilizando las leyes relativas a los movimientos planetarios que aquél estableció.

En 1628 pasó al servicio de A. von Wallenstein, en Sagan (Silesia), quien le prometió, en vano, resarcirle de la deuda contraída con él por la Corona a lo largo de los años. Un mes antes de morir, víctima de la fiebre, Kepler había abandonado Silesia en busca de un nuevo empleo

El tema de los movimientos planetarios es inseparable de un nombre: Johannes Kepler. La obsesión de Kepler por la geometría y la supuesta armonía del universo le permitieron, luego de varios frustrados intentos, enunciar las tres leyes que describen con extraordinaria precisión, el movimiento de los planetas alrededor del Sol. Desde una posición cosmológica copernicana, que como hemos visto en esa época era más una creencia filosófica que una teoría científica, Kepler logró esta magnífica empresa de manera totalmente empírica, sin más teoría que su propio convencimiento sobre el carácter fundamental (divino) de la geometría, y utilizando la gran cantidad de datos experimentales obtenidos por Tycho Brahe.

La primera ley establece, a pesar de su autor, que los planetas describen órbitas elípticas alrededor del Sol, que ocupa uno de sus focos. En la escala de valores geométricos de Kepler, el círculo ocupaba un lugar privilegiado y de ahí su decepción, luego de múltiples intentos por compatibilizar las observaciones con órbitas circulares.

Primera Ley: "La orbita que describe cada planeta es una elipse con el Sol en uno de sus focos"

Las elipses de las trayectorias sonde muy poca excentricidad, de tal manera que difieren muy poco de la circunferencia. Asì por ejemplo , la excentricidad de la órbita de la Tierra es e=0,017, y como la distancia Tierra-Sol es aproximadamente 150.000.000 de Km. la distancia del Sol (foco) al centro de la elipse es de ae=2.500.000 Km.

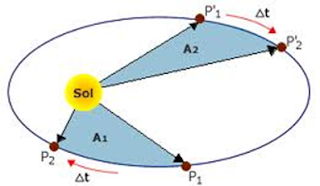
La segunda ley se refiere a las áreas barridas por la línea imaginaria que une cada planeta al Sol, llamada radio vector. Kepler observó que los planetas se mueven más rápido cuando se hallan más cerca del Sol, pero el radio vector encierra superficies iguales en tiempos iguales. (Si el planeta tarda el mismo tiempo en ir de A a B en la figura , que de c a D, las áreas en blanco son iguales).

Segunda Ley: "Cada planeta se mueve de tal manera que el radio vector (recta que une el centro del Sol con el planeta) barre área iguales en tiempos iguales"

El radio vector r, o sea la distancia entre el planeta y el foco (Sol) es variable, pues es mínima en el perihelio y máxima en el afelio. Como la velocidad areal (área barrida en la unidad de tiempo) es constante, la velocidad del planeta en su órbita debe ser variable. En virtud de esta ley, si las áreas PFM y AFN son iguales, el arco PM será menor que el AN, lo que indica que el planeta se desplaza más ligero en el perihelio. Es decir, su velocidad es máxima a la mínima distancia al Sol y mínima a la máxima distancia.

Finalmente, la tercera ley relaciona el semieje mayor de la órbita, llamado a, al período orbital del planeta p, de la siguiente manera: a3/P2 = constante. De acuerdo a esta ley, la duración de la trayectoria orbital de un planeta aumenta con la distancia al Sol y así sabemos que el “año” (definido como el tiempo empleado por el planeta en volver al mismo punto de su órbita) en Mercurio tiene 88 días (terrestres), en Venus 224, en la Tierra 365 y sigue aumentando a medida que nos alejamos del Sol. Estas leyes permiten también deducir las distancias relativas de los objetos del sistema solar, si conocemos sus movimientos. Determinando independientemente alguna de ellas es posible conocer sus valores absolutos.

Tercera Ley: "El cuadrado de los períodos de revolución de dos planetas es proporcional a los cubos de sus distancias medias al Sol."

Por primera vez una única curva geométrica, sin agregados ni componentes, y una única ley de velocidad resultan suficientes para predecir las posiciones planetarias, y por primera vez también, las predicciones son tan precisas como las observaciones.

LEY DE GRAVITACIÓN UNIVERSAL

Un momento culminante en la historia de la Física fue el descubrimiento realizado por Isaac Newton de la Ley de la Gravitación Universal: todos los objetos se atraen unos a otros con una fuerza directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que separa sus centros. Al someter a una sola ley matemática los fenómenos físicos más importantes del universo observable, Newton demostró que la física terrestre y la física celeste son una misma cosa.

El concepto de gravitación lograba de un solo golpe:

· Revelar el significado físico de las tres leyes de Kepler sobre el movimiento planetario.

· Resolver el intrincado problema del origen de las mareas

· Dar cuenta de la curiosa e inexplicable observación de Galileo Galilei de que el movimiento de un objeto en caída libre es independiente de su peso.

La naturaleza cuadrática inversa de la fuerza centrípeta para el caso de órbitas circulares, puede deducirse fácilmente de la tercera ley de Kepler sobre el movimiento planetario y de la dinámica del movimiento circular uniforme:

El sol ejerce una fuerza de atracción gravitacional sobre el planeta, pero el planeta también ejerce una fuerza de atracción gravitacional sobre el sol.

Las leyes de Kepler son una descripción del movimiento de los planetas. Nos dicen cómo se mueven, pero no por qué se mueven así.

Luego de mucho pensar en los movimientos planetarios, tema de moda en su época, Newton encontró la explicación. Los planetas, como todos los cuerpos que se mueven, tenían que obedecer en primer lugar a las leyes del movimiento que Newton había formulado hacía poco. Combinando la descripción de Kepler con sus leyes del movimiento, Newton encontró la forma matemática de la fuerza que ejerce el sol sobre los planetas. El razonamiento va así:

Los planetas se desvían del camino recto. No tienen un movimiento rectilíneo e uniforme. Por lo tanto, según la primera ley de Newton, sobre ellos actúa alguna fuerza

Una fuerza causa una aceleración (segunda ley de Newton). La aceleración que produce esa fuerza es tal que el planeta se mueve en una elipse con el sol en un foco y cumpliendo las otras dos leyes de Kepler. ¿Qué forma matemática debe tener la fuerza para producir esa aceleración?

Newton usó unas matemáticas que él mismo había inventado y concluyó que la fuerza que ejerce el sol sobre un planeta era:

Proporcional a la masa del planeta: cuanto mayor la masa del planeta, más intensa la fuerza proporcional a la masa del sol e inversamente proporcional a la distancia entre ambos, pero elevada al cuadrado: cuanto más lejos el planeta, menos intensa la fuerza.

Aquí está la forma matemática de la fuerza de gravedad:

Dónde:

G es un número fijo, llamado constante de la gravitación universal
M es la masa del sol
m es la masa del planeta
d es la distancia entre el planeta y el sol

Y, por cierto, también hay que tomar en cuenta la tercera ley de Newton (la de la acción y la reacción): si el sol ejerce una fuerza sobre el planeta, éste ejerce sobre el sol una fuerza de la misma intensidad, pero dirigida al revés.

¿Por qué entonces no gira el sol alrededor del planeta? (Pista: el sol, con masa mucho mayor, tiene inercia mucho mayor.)

La ley de la gravitación universal de Newton se pudo extender después más allá del sistema solar, a los movimientos de las estrellas y hasta al de las galaxias. Se justificaba cada vez más llamarla “universal”.

ISAAC NEWTON

Científico inglés (Woolsthorpe, Lincolnshire, 1642 - Londres, 1727). Hijo póstumo y prematuro, su madre preparó para él un destino de granjero; pero finalmente se convenció del talento del muchacho y le envió a la Universidad de Cambridge, en donde hubo de trabajar para pagarse los estudios. Allí Newton no destacó especialmente, pero asimiló los conocimientos y principios científicos de mediados del siglo XVII, con las innovaciones introducidas por Galileo, Bacon, Descartes, Kepler y otros.

Tras su graduación en 1665, Isaac Newton se orientó hacia la investigación en Física y Matemáticas, con tal acierto que a los 29 años ya había formulado teorías que señalarían el camino de la ciencia moderna hasta el siglo XX; por entonces ya había obtenido una cátedra en su universidad (1669).

Suele considerarse a Isaac Newton uno de los protagonistas principales de la llamada «Revolución científica» del siglo XVII y, en cualquier caso, el padre de la mecánica moderna. No obstante, siempre fue remiso a dar publicidad a sus descubrimientos, razón por la que muchos de ellos se conocieron con años de retraso.

Newton coincidió con Leibniz en el descubrimiento del cálculo integral, que contribuiría a una profunda renovación de las Matemáticas; también formuló el teorema del binomio (binomio de Newton). Pero sus aportaciones esenciales se produjeron en el terreno de la Física.

Sus primeras investigaciones giraron en torno a la óptica: explicando la composición de la luz blanca como mezcla de los colores del arco iris, Isaac Newton formuló una teoría sobre la naturaleza corpuscular de la luz y diseñó en 1668 el primer telescopio de reflector, del tipo de los que se usan actualmente en la mayoría de los observatorios astronómicos; más tarde recogió su visión de esta materia en la obra Óptica (1703).

También trabajó en otras áreas, como la termodinámica y la acústica; pero su lugar en la historia de la ciencia se lo debe sobre todo a su refundación de la mecánica. En su obra más importante, Principios matemáticos de la filosofía natural (1687), formuló rigurosamente las tres leyes fundamentales del movimiento: la primera ley de Newton o ley de la inercia, según la cual todo cuerpo permanece en reposo o en movimiento rectilíneo uniforme si no actúa sobre él ninguna fuerza; la segunda o principio fundamental de la dinámica, según el cual la aceleración que experimenta un cuerpo es igual a la fuerza ejercida sobre él dividida por su masa; y la tercera, que explica que por cada fuerza o acción ejercida sobre un cuerpo existe una reacción igual de sentido contrario.

De estas tres leyes dedujo una cuarta, que es la más conocida: la ley de la gravedad, que según la leyenda le fue sugerida por la observación de la caída de una manzana del árbol. Descubrió que la fuerza de atracción entre la Tierra y la Luna era directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que las separa, calculándose dicha fuerza mediante el producto de ese cociente por una constante G; al extender ese principio general a todos los cuerpos del Universo lo convirtió en la ley de gravitación universal.

La mayor parte de estas ideas circulaban ya en el ambiente científico de la época; pero Newton les dio el carácter sistemático de una teoría general, capaz de sustentar la concepción científica del Universo durante varios siglos. Hasta que terminó su trabajo científico propiamente dicho (hacia 1693), Newton se dedicó a aplicar sus principios generales a la resolución de problemas concretos, como la predicción de la posición exacta de los cuerpos celestes, convirtiéndose en el mayor astrónomo del siglo. Sobre todos estos temas mantuvo agrios debates con otros científicos (como Halley, Hooker, Leibniz o Flamsteed), en los que encajó mal las críticas y se mostró extremadamente celoso de sus posiciones.

Como profesor de Cambridge, Newton se enfrentó a los abusos de Jacobo II contra la universidad, lo cual le llevó a aceptar un escaño en el Parlamento surgido de la «Gloriosa Revolución» (1689-90). En 1696 el régimen le nombró director de la Casa de la Moneda, buscando en él un administrador inteligente y honrado para poner coto a las falsificaciones. Volvería a representar a su universidad en el Parlamento en 1701. En 1703 fue nombrado presidente de la Royal Society de Londres. Y en 1705 culminó la ascensión de su prestigio al ser nombrado caballero.