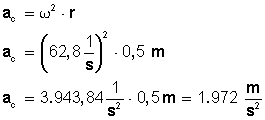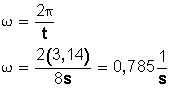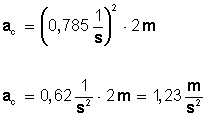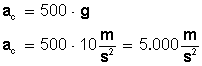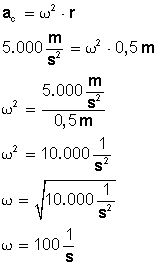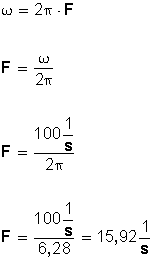"EXPLICACIÓN DE LAS LEYES DEL MOVIMIENTO O LEYES DE NEWTON"
Inercia (Primera Ley de Newton)

La inercia mecánica es la tendencia de los cuerpos a mantener el estado de movimiento o reposo en el que se encuentran. El cual no se modifica a menos que actúen fuerzas externas sobre su masa.
También puede considerarse la inercia como la tendencia de los cuerpos a mantener su estado, sea de reposo o de movimiento, hasta que una fuerza externa modifique dicho estado.
La primera ley de Newton, conocida también como Ley de inercía, nos dice que si sobre un cuerpo no actua ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero). Es decir, que si el cuerpo esta en reposo, este permanecera en reposo si no existe una fuerza externa que lo modifique.
La Dinamica (Segunda Ley de Newton)
La Inercia nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es directamente proporcional a la aceleración que adquiere dicho cuerpo e inversamente proporcional a la masa. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
F = m a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
F = m a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N.
Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m · a.
Acción y Reacción (Tercera Ley de Newton)
Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos
VIDEO 1.
VIDEO 2.
VIDEO 3
Concepto de Fuerza
la fuerza es un concepto difícil de definir, pero muy conocido. Sin que nos digan lo que es la fuerza podemos intuir su significado a través de la experiencia diaria.
 |
| Fuerza para levantar pesas. |
Una fuerza es algo que cuando actúa sobre un cuerpo, de cierta masa, le provoca un efecto.
Por ejemplo, al levantar pesas, al golpear una pelota con la cabeza o con el pie, al empujar algún cuerpo sólido, al tirar una locomotora de los vagones, al realizar un esfuerzo muscular al empujar algo, etcétera siempre hay un efecto.
El efecto de la aplicación de una fuerza sobre un objeto puede ser:
• modificación del estado de movimiento en que se encuentra el objeto que la recibe
• modificación de su aspecto físico
También pueden ocurrir los dos efectos en forma simultánea. Como sucede, por ejemplo, cuando alguien patea una lata de bebida: la lata puede adquirir movimiento y también puede deformarse.
De todos los ejemplos citados podemos concluir que:
• La fuerza es un tipo de acción que un objeto ejerce sobre otro objeto (se dice que hay unainteracción). Esto puede apreciarse en los siguientes ejemplos:
— un objeto empuja a otro: un hombre levanta pesas sobre su cabeza
— un objeto atrae a otro: el Sol atrae a la Tierra
— un objeto repele a otro: un imán repele a otro imán
— un objeto impulsa a otro: un jugador de fútbol impulsa la pelota con un cabezazo
— un objeto frena a otro: un ancla impide que un barco se aleje.
• Debe haber dos cuerpos: de acuerdo a lo anterior, para poder hablar de la existencia de una fuerza, se debe suponer la presencia de dos cuerpos, ya que debe haber un cuerpo que atrae y otro que es atraído, uno que impulsa y otro que es impulsado, uno que empuja y otro que es empujado, etc.
Dicho de otra manera, si se observa que sobre un cuerpo actúa una fuerza, entonces se puede decir que, en algún lugar, hay otro u otros cuerpos que constituyen el origen de esa fuerza.
• Un cuerpo no puede ejercer fuerza sobre sí mismo. Si se necesita que actúe una fuerza sobre mi persona, tendré que buscar algún otro cuerpo que ejerza una fuerza, porque no existe ninguna forma de que un objeto ejerza fuerza sobre sí mismo (yo no puedo empujarme, una pelota no puede "patearse" a sí misma).
• La fuerza siempre es ejercida en una determinada dirección: puede ser hacia arriba o hacia abajo, hacia adelante, hacia la izquierda, formando un ángulo dado con la horizontal, etc.
 |
| Fuerza de contacto sobre la pelota. |
Para representar la fuerza se emplean vectores. Los vectores son entes matemáticos que tienen la particularidad de ser direccionales; es decir, tienen asociada una dirección. Además, un vector posee módulo, que corresponde a su longitud, su cantidad numérica y su dirección (ángulo que forma con una línea de referencia).
Se representa un vector gráficamente a través de una flecha en la dirección correspondiente
Resumiendo:
| En física, fuerza es toda causa capaz de modificar el estado de reposo o de movimiento de un cuerpo. |
Una fuerza es una cantidad vectorial. ¿Qué significa esto?
Significa que tiene tres componentes:
— un valor, que viene dado por un número y una unidad de medida (25 Newton, por ejemplo).
— una dirección, que vendría a ser la línea de acción de la fuerza (dirección vertical, por ejemplo).
— un sentido, que vendría a ser la orientación, el hacia dónde se dirige la fuerza (hacia arriba, por ejemplo).
Estos tres componentes deben estar incluidos en la información de una fuerza.
Las fuerzas se pueden sumar y restar. No tiene sentido físico el multiplicarlas o dividirlas.
Si sumas dos fuerzas que van en la misma dirección y en el mismo sentido, entonces la suma es la suma aritmética de ellas. Si sus valores son 40 Newton y 30 Newton, el resultado sería 70 Newton en la dirección y sentido común que tienen.
Clasificación de las fuerzas
Las fuerzas se pueden clasificar de acuerdo a algunos criterios: según su punto de aplicación y según el tiempo que dure dicha aplicación.
Según su punto de aplicación:
a) Fuerzas de contacto: son aquellas en que el cuerpo que ejerce la fuerza está en contacto directo con el cuerpo que la recibe.
Un golpe de cabeza a la pelota, sujetar algo, tirar algo, etc.
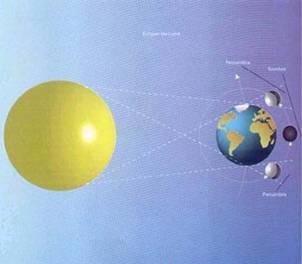 |
| Fuerzas gravitacionales a distancia entre el Sol, la Tierra y la Luna. |
b) Fuerzas a distancia: el cuerpo que ejerce la fuerza y quien la recibe no entran en contacto físicamente.
El ejemplo más familiar de una fuerza de este tipo es la atracción gravitatoria terrestre, responsable de que todos los cuerpos caigan hacia el suelo. Otro ejemplo es la fuerza que un imán ejerce sobre otro imán o sobre un clavo.
Según el tiempo que dura la aplicación de la fuerza:
a) Fuerzas impulsivas: son, generalmente, de muy corta duración, por ejemplo: un golpe de raqueta.
b) Fuerzas de larga duración: son las que actúan durante un tiempo comparable o mayor que los tiempos característicos del problema de que se trate.
Por ejemplo, el peso de una persona es una fuerza que la Tierra ejerce siempre sobre la persona. La fuerza que ejerce un cable que sostiene una lámpara, durará todo el tiempo que la lámpara esté colgando de ese cable. La fuerza que ejerce el cable sobre un teleférico durará mientras ahí esté.
Asimismo, las fuerzas que actúan sobre un cuerpo pueden ser exteriores e interiores.
a) Fuerzas exteriores: son las que actúan sobre un cuerposiendo ejercidas por otros cuerpos.
 |
| Fuerza impulsiva aplicada sobre la pelota. |
b) Fuerzas interiores: son las que una parte de un cuerpo ejerce sobre otra parte de si mismo.
Unidades de fuerza
El primer paso para poder cuantificar una magnitud física es establecer una unidad para medirla.
En el Sistema Internacional (SI) de unidades la fuerza se mide en newtons(símbolo: N), en el CGS en dinas (símbolo, dyn) y en el sistema técnico enkilopondio (símbolo: kp), siendo un kilopondio lo que comúnmente se llama un kilogramo, un kilogramo fuerza o simplemente un kilo.
Un newton es la fuerza que, al ser aplicada a un cuerpo de masa 1 Kilogramo, le comunica una aceleración de 1 metro por segundo al cuadrado.
|
Fuerza normal
La fuerza normal es aquella que ejerce una superficie como reacción a un cuerpo que ejerce una fuerza sobre ella.Si la superficie es horizontal y no hay otra fuerza actuando que la modifique (como por ejemplo la tensión de una cuerda hacia arriba), la fuerza normal es igual al peso pero en sentido contrario. En este caso una fuerza horizontal empujando el cuerpo no modifica la normal. En un plano inclinado la normal es una proyección del peso.Generalizando, la fuerza normal es una fuerza de reacción de la superficie en sentido contrario a la fuerza ejercida sobre la misma.
La fuerza normal no es un par de reacción del peso, sino una reacción de la superficie a la fuerza que un cuerpo ejerce sobre ella.
Fuerza de rozamiento
La
fuerza de rozamiento es una fuerza que aparece cuando hay doscuerpos en contacto y es una fuerza muy importante cuando se estudia elmovimiento de los cuerpos. Es la causante, por ejemplo, de que podamos andar(cuesta mucho más andar sobre una superficie con poco rozamiento, hielo, porejemplo, que por una superficie con rozamiento como, por ejemplo, un suelorugoso).

Existe rozamiento incluso cuando no hay movimiento relativo entre los doscuerpos que están en contacto. Hablamos entonces de
Fuerza de rozamiento estática. Por ejemplo, si queremos empujar un armario muy grande y hacemosuna fuerza pequeña, el armario no se moverá. Esto es debido a la fuerza de rozamiento estática que se opone al movimiento. Si aumentamos la fuerza con laque empujamos, llegará un momento en que superemos está fuerza de rozamiento yserá entonces cuando el armario se pueda mover, tal como podemos observar enla animación que os mostramos aquí. Una vez que el cuerpo empieza a moverse,hablamos de
fuerza de rozamiento dinámica. Esta fuerza de rozamientodinámica es
menor que la fuerza de rozamiento estática.
La experiencia nos muestra que:
- la fuerza de rozamiento entre dos cuerpos no depende del tamaño de la superficie de contacto entre los dos cuerpos, pero sí depende de cúal sea la naturaleza de esa superficie de contacto, es decir, de que materiales la formen y si es más o menos rugosa.
- la magnitud de la fuerza de rozamiento entre dos cuerpos en contacto es proporcional a la normal entre los doscuerpos, es decir:
Fr = m·N
donde m es lo que conocemos como coeficiente de rozamiento.
Hay dos coeficientes de rozamiento: el
estático, me, y el
cinético, mc, siendo el primero mayor que el segundo:
me > mc
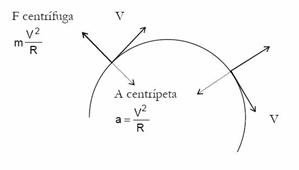
Fuerzas centrípeta y centrífuga
Todas las fuerzas que actúan sobre un vehículo son importantes, pero de entre todas ellas, las que podemos llegar a percibir con mayor intensidad son las fuerzas "centrípeta" y "centrífuga".
Cuando ambas fuerzas permanecen en equilibrio al realizar un movimiento circular, es decir, al girar en una curva, el paso por ella se resliza sin sobresaltos, pero cuando el equilibrio se rompe y una de las fuerzas supera al otra, nuestra trayectoria se modifica pudiendo derivar en una salida violenta de la calzada y la eventualidad de un peligroso accidente.
Al hablar del centro de gravedad, hemos mencionado el "anillo" como una forma "especial", al tener aquél, fuera de si mismo. Los anillos y su expresión lineal; "la circunferencia", tienen una especial transcendencia, ya que cuando conducimos cualquier vehículo, cambiamos de dirección mediante giros, curvas... anillos, en una palabra.
Todos, alguna vez, hemos hecho girar una cuerda asiéndola por un extremo y colocando algún objeto pesado en el otro. El efecto producido es un movimiento circular con unas características muy interesantes.
Si pudiéramos fotografiar el movimiento lo suficientemente rápido como para descomponerlo "paso a paso", observaríamos que en cada uno de ellos, el objeto del extremo cambia de dirección.
Recordando el ejemplo del juguete, cuando le dimos el puntapié lo impulsamos hacia delante aplicándole una fuerza y el movimiento, hasta que se vio frenado por la alfombra y el rozamiento, el movimiento fue rectilíneo. Si hubiésemos que modificase su trayectoria, tendríamos que haberle dado otro puntapié que cambiase su trayectoria lateralmente. En otras palabras, tendríamos que haberle aplicado otra fuerza orientada en una dirección distinta.

Por tanto, para que un cuerpo cambie de dirección, es necesario que reciba una fuerza. Si el objeto de la cuerda cambia constantemente de dirección es por estar recibiendo en cada momento una fuerza que le obliga a hacerlo.
Nuestra sensación mientras giramos la cuerda, es que algo está tirando de nuestra mano como si quisiera escapar de ella, arrastrándonos y haciéndonos girar con ella hacia fuera. Cuando vemos a un lanzador de martillo, parece que va a salir disparado detrás de éste en el momento de soltarlo después de hacerlo girar con fuerza.
Este fenómeno no es otro que la "fuerza centrífuga", que operando desde el centro de giro, (nuestra mano) impulsa el objeto hacia el exterior y esto no sucede porque otra fuerza dirigida en sentido contrario, anula a la anterior, impidiéndolo. Esa otra fuerza "oposición" se llama "centrípeta" y está dirigida "de fuera, hacia adentro". El resultado de la pugna entre ambas fuerzas y el impulso que le hemos dado, es un movimiento circular.

La conclusión para nosotros, conductores de un vehículo, es que, al abordar una curva, un giro o un cambio de dirección, estaremos sometidos a la acción de las fuerzas centrífuga y centrípeta. Mientras estas dos fuerzas se mantengan en equilibrio, pasaremos por la curva con éxito, en el caso contrario visitaremos al cuneta. Es, por tanto lógico pensar, que cuanto más brusco es el cambio de dirección, más intensa será la fuerza centrífuga.
Cuando hablamos de vehículos, la "cuerda" que nos mantiene sobre la carretera se conoce como "adherencia", que es la propiedad que tienen los neumáticos para permanecer en contacto con el suelo. Si el cambio de dirección es muy brusco, la fuerza ejercida sobre la "cuerda" puede hacer que ésta se rompa. Por esta razón, al abordar curvas, debemos calcular mentalmente, la velocidad adecuada para superarlas sin peligro. Conforme la curva sea más cerrada, menor deberá ser la velocidad de paso por ella
TALLER DE APLICACIÓN
PRIMERA LEY DE NEWTON, LEY DE LAINERCIA
1) ¿Has tratado de bajarte de un carrusel antes de que pare? Es mejor que no lo hagas porque te puedes golpear.
a) ¿Cómo explica esto un hombre de ciencia?
b) ¿Que fuerza hace que te caigas del carrusel?
2) ¿Qué sensación percibes cuando el auto aumenta su velocidad o se detienes bruscamente? Descríbelas
3) ¿Cómo puedes juzgar si sobre un cuerpo está actuando una fuerza neta diferente de cero?
4) si un cuerpo se encuentra en reposo, ¿puedes llegar a la conclusión que sobre él no actúa ninguna fuerza?
5) si un cuerpo se mueve con MU, ¿puedes concluir que la fuerza que actúa sobre el esconstante?6) si solo actúa una fuerza sobre un cuerpo, ¿podrá el cuerpo desplazarse con velocidad constante?
7) si sobre un cuerpo actúan dos fuerzas ¿bajo qué condiciones podrá el cuerpo permanecer en reposo con movimiento uniforme?
8) si un cuerpo posee movimiento circular uniforme, ¿existirá una fuerza neta actuando sobre él?
9) si un cuerpo cae libremente desde cierta altura ¿existirá una fuerza neta actuando sobre él?
10) si un cuerpo describe un movimiento parabólico ¿qué fuerza neta actúa sobre él?
11) Es posible que un cuerpo describa en su movimiento una curva cualquiera sin que actué sobre él una fuerza neta?
12) una cuerda puede sostener justamente una masa de 1kg suspendida en reposo ¿se romperá la cuerda si la masa se pone a oscilar en forma de péndulo?
SEGUNDA LEY DE NEWTON
1) imagina un cuerpo que se mueve con velocidad constante a lo largo de una trayectoria rectilínea horizontal.
a) Si una fuerza empuja el cuerpo en la dirección del movimiento, la velocidad del cuerpo ¿aumentara, disminuirá o continuara igual?
b) Cuando la fuerza adicional deje de actuar ¿Qué pasa con la velocidad del cuerpo?
c) ¿Qué pasara con la velocidad del cuerpo si la fuerza adicional actúa en dirección contraria al movimiento?
2) dibuja la fuerza resultante que actúa sobre un cuerpo cuyo movimiento es:
a) Rectilíneo uniforme
b) Uniformemente acelerado
c) Parabólico
d) Circular
3) ¿qué fuerza se debe ejercer sobre un cuerpo de 12kg de masa para que se acelere a razón de 3,5 m/s2?
4) sobre un cuerpo de 8kg de masa ejercen fuerzas de 12N y 5N que forman entre si un ángulo de 90°. Calcular la fuerza resultante que actúa sobre el cuerpo y la aceleración que experimenta.
5) sobre un cuerpo de 4kg de masa, inicialmente en reposo, actúa una fuerza de32N ¿Qué velocidad llevara el cuerpo cuando ha recorrido 14m?
6) ¿si sobre un cuerpo actúa una fuerza de 54N, este se acelera a razón de 9 m/s’ ¿Cuánto se acelerara si la fuerza aplicada fuera de 6N?
7) dos personas halan de un cuerpo de 20kgcon fuerzas de 100N y 200N calcular la aceleración de la masa si:
a) Las fuerzas se ejercen horizontalmente en el mismo sentido
b) Las fuerzas actúan horizontalmente en sentido contrario
c)Las fuerzas forman entre si un ángulo de 60°
8) ¿Cómo será el cambio de la aceleración si disminuye la masa?
TERCERA LEY DE NEWTON
1. La universalidad de la tercera ley de Newton permite la explicación física de muchos hechos de la vida cotidiana, desde el más elemental como sostenernos sobre la tierra, hasta el movimiento de los cohetes que se aventuran fuera de la atracción gravitacional. Analiza el porqué de cada uno de los siguientes fenómenos.
a ¿Por qué una persona se mantiene sobre la tierra?
b. ¿Por qué puede saltar una persona y porque lo hace?
c. ¿Por qué puede una persona caminar sobre la tierra?
d. ¿Cómo funciona un cohete?
e. ¿Cómo hace una lancha de motor para desplazarse sobre el agua?
2. Indaga sobre otros hechos cuya explicación necesite de la tercera ley de Newton
3. Dibuja por medio de vectores el par de fuerzas de acción y reacción en las siguientes situaciones:
a. Golpear una mesa con el puño
b. Un globo desinflándose
c. Una mano sosteniendo un objet
4. Dos estudiantes A y B, montando cada uno sobre un par de patines, se encuentran unidos por una cuerda y sobre una superficie horizontal y lisa si A tira de la cuerda ejerciendo sobre B una fuerza F.
a. Describa físicamente que le sucede al estudiante B
b. Describa físicamente que le sucede al estudiante A
c. ¿Qué relación existe entre la fuerza ejercida por A sobre B y la fuerza ejercida por B sobre A? ¿Cuál de las dos es mayor? ¿Cuál actúa primero? ¿Cuál es la acción y cuál es la reacción?
5. Ahora los dos estudiantes se encuentran uno frente al otro. Si B empuja a A con una fuerza F:
a. ¿Qué le sucede al estudiante A?
b. ¿Qué le sucede al estudiante A?
c. Si en lugar del estudiante A existiera una pared la fuerza ejercida sobre B, ¿sería igual o diferente?
6. De acuerdo con la primera ley de Newton para que un cuerpo cambie su estado de movimiento debe actuar sobre él una fuerza externa, explica físicamente por qué un carro se puede mover en forma acelerada, recuerde que un cuerpo no puede ejercer fuerza sobre sí mismo
7. Un problema típico relativo a la tercera ley de newton es el planteado por el caballo y el cochero:
Después de una clase de física en la escuela de animales, el caballo se rehúsa a continuar la marcha cuando es golpeado por el cochero, ante la insistencia del amo, el caballo cita en su defensa la tercera ley Newton: cuando yo hago fuerza para tirar el coche, este a su vez hace una fuerza sobre mí con la misma magnitud pero diferente sentido. Si pretendo aumentar la fuerza la reacción ejercida por el coche aumenta en la misma magnitud. De esta forma es imposible poner el coche en movimiento. En consecuencia lo mejor es que no me golpee, ya que físicamente no puedo hacer absolutamente nada. En la práctica vemos que si es posible tener al caballo y al coche en movimiento acelerado, ¿Cómo explicas físicamente este hecho?¿Falla la tercera ley de newton?¿Sera que no siempre la reacción compensa la fuerza de la acción
8. Dibuja los pares acción reacción sobre cada una de los siguientes sistemas
a. Un objeto sobre una superficie
b. Un cuerpo sobre una superficie horizontal que está siendo arrastrado por medio de una cuerda de masa despreciable.
c. El sol y la tierra
d. Dos carros unidos por medio de un resorte
e. Un cuerpo en un plano inclinado
f. Una lancha
g. Un cohete.
"Recuerda que debes desarrrollarlo y manejarlo para sustentación oral o escrita".
Loperena J. T Grados 10 ABC
Licenciado Especilista: Lizandro Mejia M.









 Existe rozamiento incluso cuando no hay movimiento relativo entre los doscuerpos que están en contacto. Hablamos entonces de Fuerza de rozamiento estática. Por ejemplo, si queremos empujar un armario muy grande y hacemosuna fuerza pequeña, el armario no se moverá. Esto es debido a la fuerza de rozamiento estática que se opone al movimiento. Si aumentamos la fuerza con laque empujamos, llegará un momento en que superemos está fuerza de rozamiento yserá entonces cuando el armario se pueda mover, tal como podemos observar enla animación que os mostramos aquí. Una vez que el cuerpo empieza a moverse,hablamos de fuerza de rozamiento dinámica. Esta fuerza de rozamientodinámica esmenor que la fuerza de rozamiento estática.
Existe rozamiento incluso cuando no hay movimiento relativo entre los doscuerpos que están en contacto. Hablamos entonces de Fuerza de rozamiento estática. Por ejemplo, si queremos empujar un armario muy grande y hacemosuna fuerza pequeña, el armario no se moverá. Esto es debido a la fuerza de rozamiento estática que se opone al movimiento. Si aumentamos la fuerza con laque empujamos, llegará un momento en que superemos está fuerza de rozamiento yserá entonces cuando el armario se pueda mover, tal como podemos observar enla animación que os mostramos aquí. Una vez que el cuerpo empieza a moverse,hablamos de fuerza de rozamiento dinámica. Esta fuerza de rozamientodinámica esmenor que la fuerza de rozamiento estática.

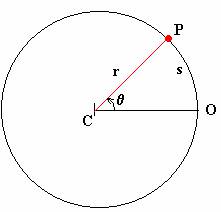


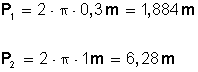
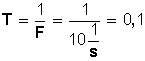 s (Período)
s (Período)