MOVIMIENTO CIRCULAR
Se define como movimiento circular aquél cuya trayectoria es una circunferencia.
El movimiento circular, llamado también curvilíneo, es otro tipo de movimiento sencillo.
Estamos rodeados por objetos que describen movimientos circulares: un disco compacto durante su reproducción en el equipo de música, las manecillas de un reloj o las ruedas de una motocicleta son ejemplos de movimientos circulares; es decir, de cuerpos que se mueven describiendo una circunferencia.
A veces el movimiento circular no es completo: cuando un coche o cualquier otro vehículo toma una curva realiza un movimiento circular, aunque nunca gira los 360º de la circunferencia.
La experiencia nos dice que todo aquello da vueltas tiene movimiento circular. Si lo que gira da siempre el mismo número de vueltas por segundo, decimos que posee movimiento circular uniforme (MCU).
El radián
Si tenemos un ángulo cualquiera y queremos saber cuánto mide, tomamos un transportador y lo medimos. Esto nos da el ángulo medido en grados. Este método viene de dividir la circunferencia en 360º, y se denomina sexagesimal.
(Para usar la calculadora en grados hay que ponerla en DEG, Degrees, que quiere decir grados en inglés).
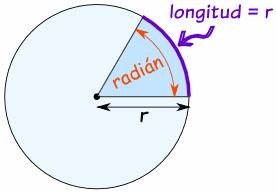
El sistema de grados sexagesimales es una manera de medir ángulos, pero hay otros métodos, y uno de ellos es usando radianes.
Ahora veamos el asunto de medir los ángulos pero en radianes.
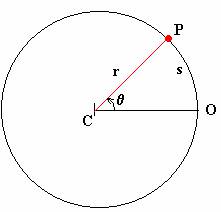
Para medir un ángulo en radianes se mide el largo del arco (s) abarcado por el ángulo θ de la figura a la izquierda. Esto se puede hacer con un centímetro, con un hilito o con lo que sea. También se mide el radio del círculo.
Para obtener el valor del ángulo (θ) en radianes usamos la fórmula:
y tenemos el ángulo medido en radianesHacer la división del arco sobre radio significa ver cuántas veces entra el radio en el arco. Como el radio y el arco deben medirse en la misma unidad, el radián resulta ser un número sin unidades.
Esto significa que el valor del ángulo en radianes solo me indica cuántas veces entra el radio en el arco. Por ejemplo, si el ángulo θ mide 3 radianes, eso significa que el radio entra 3 veces en el arco abarcado por ese ángulo.
Su quisiéramos calcular o conocer al valor del arco, hacemos:
 |
| ¿Cuántas veces entra el radio en el arco marcado? |
¿A cuántos grados equivale un radián?
Pero el valor de un ángulo en radianes se puede expresar (convertir) en grados. En una circunferencia entera (360º) el arco entero es el perímetro, que es igual a 2 Pi por radio
. Así, a partir de la fórmulaes que 360° equivalen a:
Un ángulo de un radián equivale a un ángulo de 57,3º.
Para usar la calculadora en radianes hay que ponerla en "RAD"
Periodo y frecuencia
La principal característica del movimiento circular uniforme es que en cada vuelta o giro completo de 360°, equivalente a un ciclo, se puede establecer un punto fijo como inicio y fin del ciclo.
En física, los ciclos son también llamados revoluciones para un determinado tiempo.
El periodo (T) de un movimiento circular es el tiempo que tarda una partícula o un cuerpo en realizar una vuelta completa, revolución o ciclo completo.
Por ejemplo, el periodo de rotación de la tierra es 24 horas. El periodo de rotación de la aguja grande del reloj es de 1 hora. La unidad utilizada para el periodo es el segundo o, para casos mayores, unidades mayores.
Conocida la frecuencia (en ciclos o revoluciones por segundo) se puede calcular el periodo (T) mediante la fórmula:
Se denomina frecuencia (F) de un movimiento circular al número de revoluciones, vueltas o ciclos completos durante la unidad de tiempo. La unidad utilizada para cuantificar (medir) la frecuencia de un movimiento es el hertz (Hz), que indica el número de revoluciones o ciclos por cada segundo.
Para su cálculo, usamos la fórmula
o hertz:La velocidad angular (ω)
Cuando un objeto se mueve en una circunferencia, llevará una velocidad, ya que recorre un espacio, pero también recorre un ángulo.
Para tener una idea de la rapidez con que algo se está moviendo con movimiento circular, se ha definido la velocidad angular (ω) como el número de vueltas que da el cuerpo por unidad de tiempo.
Si un cuerpo tiene gran velocidad angular quiere decir que da muchas vueltas por segundo.
De manera sencilla: en el movimiento circular la velocidad angular está dada por la cantidad de vueltas que un cuerpo da por segundo.
Otra manera de decir lo mismo sería: en el movimiento circular la velocidad angular está dada por el ángulo recorrido (θ) dividido por unidad de tiempo. El resultado está en grados por segundo o en rad por segundo.
ω = velocidad angular en rad/seg.
θ = desplazamiento angular en rad.
t = tiempo en segundos en que se efectuó el desplazamiento angular.
La velocidad angular también se puede determinar si sabemos el tiempo que tarda en dar una vuelta completa o periodo (T):
Como
entonces 
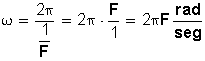
La velocidad tangencial (v)
Aparte de la velocidad angular, también es posible definir la velocidad lineal de un móvil que se desplaza en círculo.
Por ejemplo, imaginemos un disco que gira. Sobre el borde del disco hay un punto que da vueltas con movimiento circular uniforme.
Ese punto tiene siempre una velocidad lineal que es tangente a la trayectoria. Esa velocidad se llama
velocidad tangencial.
Para calcular la velocidad tangencial hacemos: espacio recorrido sobre la circunferencia (o arco recorrido) dividido por el tiempo empleado, que expresamos con la fórmula:
pero como 
entonces 
que se lee velocidad tangencial es igual a velocidad angular multiplicada por el radio.Como la velocidad angular (ω) también se puede calcular en función del periodo (T) con la fórmula
y la velocidad tangencial siempre está en función del radio, entonces la fórmula se convierte en 
que se lee: la velocidad tangencial es igual a 2 pi multiplicado por el radio (r) y dividido por el periodo (T).Además, como ω (velocidad angular) se expresa en
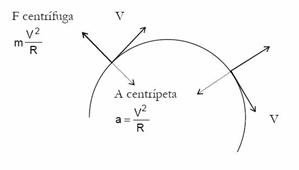
y el radio se expresa en metros, las unidades de la velocidad tangencial serán metros por segundo (m/seg).La aceleración centrípeta se calcula por cualquiera de las siguientes dos maneras:
La aceleración asociada a los cambios en su módulo (rapidez)
Resumiendo: si un móvil viaja en círculo con velocidad variable, su aceleración se puede dividir en dos componentes: una aceleración de la parte radial (la aceleración centrípeta que cambia la dirección del vector velocidad) y una aceleración angular que cambia la magnitud del vector velocidad, además de una aceleración tangencial si consideramos solo su componente lineal.
Aplicaciones del MCU
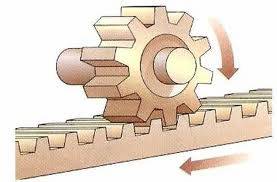
El movimiento circular del piñón se transforma en movimiento lineal en la cremallera.
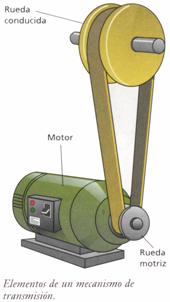
Trasmisión de un movimiento circular.
Trasmisión de un movimiento circular.
1. Un móvil con trayectoria circular recorrió 820° ¿Cuántos radianes son?
Desarrollo
Sabemos que 1 rad = 57,3°
Entonces
 |
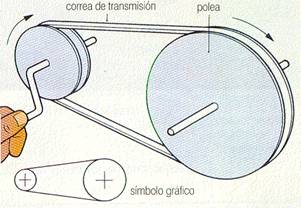| Como en un tractor, la rueda delantera es más chica. |
Desarrollo:
En este ejercicio la longitud (distancia, espacio) que recorre cada rueda en una vuelta corresponde al perímetro de cada una (perímetro del círculo), cuya fórmula es
, entonces:
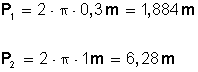
Entonces, si en una vuelta la rueda delantera recorre 1,884 metro, en 15 vueltas recorrerá: 15 • 1,884 m = 28,26 m
¿Cuantas veces la rueda trasera ha tenido que girar (dar una vuelta) para recorrer esa distancia de 28,26 m?
Dividimos esa distancia por la distancia recorrida en una vuelta por la rueda trasera:
28,26 m : 6,28 m = 4,5 vueltas.
Por lo tanto, la rueda trasera ha tenido que dar cuatro vueltas y media para recorrer la misma distancia que la delantera ha recorrido en 15 vueltas.
3. Un automóvil recorre la circunferencia de 50 cm de radio con una frecuencia F de 10 hz.
Determinar:
a) el periodo.
b) la velocidad angular.
c) su aceleración.
Una frecuencia de 50 hz es una frecuencia de 50 1/s. Para su desarrollo, sólo debemos aplicar formulas.
Sabemos que
, entonces
, velocidad angular (039)El período T es
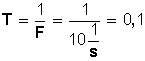s (Período)Conocemos la velocidad angular y el radio, podemos calcular la velocidad tangencial:
, velocidad tangencial.Su aceleración va a ser la aceleración centrípeta, que siempre esta apuntando hacia el centro de la circunferencia. El módulo de esta aceleración se puede calcular por cualquiera de las siguientes dos fórmulas:
Usando la segunda:
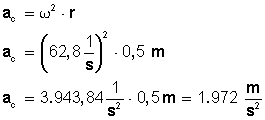
4. ¿Cuál es la aceleración que experimenta un niño que viaja en el borde de un carrusel que tiene 2 m de radio y que da una vuelta cada 8 segundos?
Si el niño da 1 vuelta cada 8 segundos su velocidad angular va a ser:
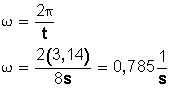
Para calcular la aceleración centrípeta tenemos
Entonces:
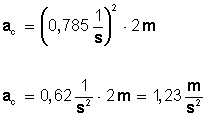
Es la aceleración centrípeta del niño.
5. Calcular la velocidad angular y la frecuencia con que debe girar una rueda, para que los puntos situados a 50 cm de su eje estén sometidos a una aceleración que sea 500 veces la de la gravedad.
Veamos los datos:
Necesitamos que la aceleración centrípeta sea igual a 500 g:
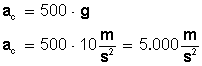
La velocidad angular para la cual se cumpla esto va a ser:
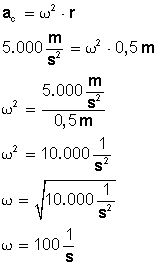
Ahora calculamos la frecuencia (F) a partir de
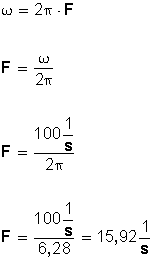
EJEMPLOS
1- Un automóvil, cuyo velocímetro indica en todo instante 72 km/h, recorre el perímetro de una pista circular en un minuto. Determinar el radio de la misma. Si el automóvil tiene una aceleración en algún instante, determinar su módulo, dirección y sentido.
Hagamos un dibujito. Visto desde arriba el asunto se ve así:
Ahora, w es 2π sobre T , entonces:
W = 2π = 2π = 0,104 1 velocidad angular
T = 60 s
Por otro lado la velocidad tangencial es 20 m/s (=72 km/h).reemplazando:
VT = w. R
R= VR = 20m/s
W = 0,104 1/s
R = 191 m Radio de la pista
- ¿Si el automóvil tiene aceleración? Rta: Sí, tiene aceleración centrípeta de modulo:
acp = w2 R = (0,104 Vs)2. 191 m
acp = 2,09 m/s2 (dirigida hacia el centro de la pista)
2- Un automóvil recorre la circunferencia de 50 cm de radio con una frecuencia F de 10hz. Determinar:
a- el periodo.
b- la velocidad angular.
c- su aceleración.
Una frecuencia de 50 hz es una frecuencia de 50 1/s. Acá sólo es cuestión de aplicar formulas. A ver si me seguís. W era 2π x f. Entonces:
W = 2π.f = 2.π 10 1/s = 62,8 1/s velocidad angular
El período T era 1/frecuencia:
T = 0,1 s Período
F =10 1/s
VR= W . R VT = 62,8 1/S X 0.5M
Vr = 31,4 m/s velocidad tangencial
Su aceleración va a ser la aceleración centrípeta, que siempre está apuntando hacia el centro de la circunferencia. El módulo de esta aceleración se puede calcular por cualquiera de las formulas: acp = w2 /R
3- cuál es la aceleración que experimenta un chico que viaja en el borde de una calesita de 2m de radio y que da vuelta cada 8 segundos.
Para calcular la aceleración centrípeta es siempre lo mismo acp= w2. R. Si el tipo da 1 vuelta cada 8 segundos su velocidad angular va a ser:
w= 2π = 0,785 1/s
t = 8s
Entonces:
acp= (0,785 1/s)2.2m
acp = 1,23 m/s2 aceleración centrípeta del chico
4- calcular la velocidad angular y la frecuencia con que debe girar una rueda, para que los puntos situados a 50cm de su eje estén sometidos a una aceleración que sea 500 veces la de la gravedad.
Este problema no es difícil. Quiero que la aceleración centrípeta sea igual a 500 g. Para que tengas una idea 500 g es el valor de una centrifugadora de laboratorio.
acp= 500.g =500 x 10 m/s2
acp= 5000 m/s2
La velocidad angular para la cual se cumpla esto va a ser:
la frecuencia será: w = 2π. f = w/2π = 100 1/s/2π
f = 15,9 1/s
TALLER DE APLICACIÓN
Resuelve los siguientes problemas, para ello sigue las estrategias de resolución de problemas:
- Planteo (datos)
- Realizar un gráfico que ilustre la situación problema
- Desarrollo, explicando los procesos realizados
- Respuesta
Realice el taller y preparelo para la Comprobación Escrita. (ENTREGAR EN GRUPOS DE DOS O TRES)
1. Un satélite de comunicaciones geoestacionario (estos satélites tienen un período de 24 horas y, por eso, siempre están sobre un mismo punto de la tierra) gira alrededor de nuestro planeta a una distancia de la superficie de la tierra de 46000 Km (el radio de la tierra es de 6.375 Km ).
a. ¿Cuál es la velocidad angular del satélite?
b. ¿Cuál es el módulo de la velocidad lineal?
2. ¿Cuántas r.p.m son 4 rad/s?
3. Calcula el período, la frecuencia y la velocidad angular de cada una de las tres manecillas de un reloj?
4. Un cazador utiliza una pequeña piedra sujeta al extremo de una cuerda como honda primitiva. Se hace girar la piedra por arriba de su cabeza en una circunferencia horizontal de 1.6m de diámetro y con una rapidez de 6 revoluciones por segundo. ¿cuál es la aceleración centrípeta de la cuerda?
5. La órbita de la Luna respecto a la tierra es aproximadamente circular, con un radio promedio de 3,84X
a. La rapidez orbital media de la Luna.
b. Su aceleración centrípeta.
6. En el ciclo de secado de una lavadora, el tubo de radio 0,30m desarrolla una rapidez de 630 rpm. ¿Cuál es la rapidez lineal máxima con la cual el agua sale de la máquina?
7. En un reloj, el minutero mide 40 mm. Hallar:
a. La frecuencia
b. El período
c. La velocidad tangencial
d. Velocidad Angular
e. Aceleración Centrípeta
a. La frecuencia
b. El período
c. La velocidad tangencial
d. Velocidad Angular
e. Aceleración Centrípeta
8. Hallar la velocidad tangencial de La Tierra (Imagina, con qué velocidad saldría la Tierra si repentinamente cesara la atracción provocada por el Sol). Investigar el radio de la tierra
9. ¿Cuántos rad/s son 25 r.p.m?
10. Un disco gira a 45 r.p.m, calcula el tiempo que tarda en dar una vuelta, así como su frecuencia.
11. Las ruedas de un automóvil de 70 cm de diámetro gira a razón de 100 r.p.m. Calcula la velocidad (lineal) de dicho automóvil.
12. Un automóvil circula a 72 km/h por una curva de 20 m de radio. ¿Cuál es su aceleración centrípeta?
13. ¿Cuántas vueltas dará el plato de un microondas en un minuto si gira a 3,5 rad/s?
14. Una rueda de 10 cm de radio gira a 3 rad/s Calcula la velocidad lineal de un punto de la periferia así como de otro punto situado a 5 cm del eje de giro.
15. Dos poleas de 8 y 12 cm de radio respectivamente, giran conectadas por una banda. Si la frecuencia de la polea de menor radio es 20vueltas/segundo, ¿cuál será la frecuencia de la polea de mayor radio?
16. Una esfera de 5 cm de radio gira a 4 rad/s. Calcula la velocidad y la aceleración de un punto situado en el ecuador de la esfera.
17. El CD de un ordenador gira a razón de 539 r.p.m. Calcula el numero de vueltas que da durante la reproducción de una canción de 4 minutos.
18. La Tierra completa una vuelta alrededor del Sol cada 365 días. Si la distancia media al Sol es 149.600.00 km. Calcula la velocidad lineal de la Tierra en torno al Sol.
profe para cuando es eso
ResponderEliminar